순열(Permutation)이란?
순열이란, 쉽게 말해서 순서를 정해서 나열하는 것을 말한다.
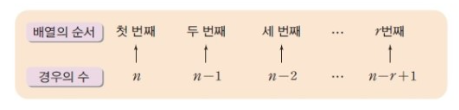
서로 다른 n개에서 r개를 택하여 일렬로 나열할 때, 첫 번째 자리에 올 수 있는 것은 n가지이고, 그 각각에 대하여 두 번째 자리에 올 수 있는 것은 첫 번째 자리에서 선택된 1개를 제외한 (n - 1) 가지, 세 번째 자리에 올 수 있는 것은 앞에서 선택된 2개를 제외한 (n - 2) 가지이다. 이와 같은 방법으로 계속하며 r번째 자리에 올 수 있는 것은 이미 선택된 (r - 1) 개를 제외한
n - (r - 1) = n - r + 1(가지)
이다.
순열에서 P란 Permutation의 첫글자를 줄여서 P로 나타낸다.
nPr을 계산하는 방법은 배열의 순서를 생각하여 첫 번째에는 나올 수 있는 경우의 수가 n개, 두 번째는 n-1개,...
r번째에는 n-r+1가 나오게 된다. 이렇게 나온 모든 경우의 수를 곱하는 것이 nPr을 구하는 방법이다.
4P3 = 4 * 3 * 2 = 24가지


C#으로 구현한 순열
nPr로 작성하면 원하는 값을 얻을 수 있다.
public class Program
{
public static void Main()
{
int[] ints = { 1, 2, 3, 4 };
Permute(ints, 0, 4, 2);
}
public static void Permute(int[] array, int depth, int n, int r)
{
if (depth == r)
{
for(int i = 0; i < r; i++)
{
Console.Write($"{array[i]} ");
}
Console.WriteLine();
}
else
{
for(int i = depth; i < n; i++)
{
swap(ref array[depth], ref array[i]);
Permute(array, depth + 1, n, r);
swap(ref array[depth], ref array[i]);
}
}
}
public static void swap(ref int a, ref int b)
{
var temp = a;
a = b;
b = temp;
}
}
재귀 과정
코드를 순서대로 따라가보자
- depth = 0
- 1과 1 스왑된다 {1,2,3,4}
- depth = 1
- 2과 2 스왑된다 {1,2,3,4}
- depth = 2
- 3과 3 스왑된다 {1,2,3,4}
- depth = 3
- depth가 3에 도달하면서 결과를 출력한다.
- {1,2,3}

- depth = 0
- 1과 1 스왑된다 {1,2,3,4}
- depth = 1
- 2과 2 스왑된다 {1,2,3,4}
- depth = 2
- 3과 4 스왑된다 {1,2,4,3}
- depth = 3
- depth가 3에 도달하면서 결과를 출력한다.
- {1,2,4}
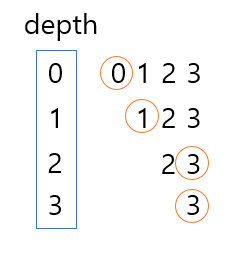
- depth = 0
- 1과 1 스왑된다 {1,2,3,4}
- depth = 1
- 2과 3 스왑된다 {1,3,2,4}
- depth = 2
- 4과 4 스왑된다 {1,3,2,4}
- depth = 3
- depth가 3에 도달하면서 결과를 출력한다.
- {1,3,2}

- depth = 0
- 1과 1 스왑된다 {1,2,3,4}
- depth = 1
- 2과 3 스왑된다 {1,3,2,4}
- depth = 2
- 2과 4 스왑된다 {1,3,4,2}
- depth = 3
- depth가 3에 도달하면서 결과를 출력한다.
- {1,3,4}

이러한 순서로 재귀를 반복...
조합(Combination)이란?
일반적으로 서로 다른 n개에서 순서를 생각하지 않고 r개를 택하는 것을 n개에서 r개를 택하는 조합이라 하고, 이 조합의 수를 기호로 nCr와 같이 나타낸다.

C#으로 구현한 조합
public class Program
{
public static void Main()
{
int[] ints = { 1, 2, 3, 4 };
int[] comb = new int[3];
Combination(ints, comb, 3, 0, 0);
}
public static void Combination(int[] array, int[] comb, int r, int index, int depth)
{
if (r == 0)
{
for (int i = 0; i < comb.Length; i++)
{
Console.Write($"{comb[i]}");
}
Console.WriteLine();
}
else if (depth == array.Length)
{
return;
}
else
{
comb[index] = array[depth];
Combination(array, comb, r - 1, index + 1, depth + 1);
Combination(array, comb, r, index, depth + 1);
}
}
}
더 쉬운 버전
using System;
using System.Collections.Generic;
using System.Text;
public class Combination
{
private int n;
private int r;
private List<int> list = new List<int>();
private int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
public Combination(int n, int r)
{
this.n = n;
this.r = r;
for (int i = 0; i < r; i++)
{
list.Add(0);
}
}
public void DoCombination(int now, int pos)
{
if (now == r)
{
for (int i = 0; i < r; i++)
{
Console.Write(arr[list[i]] + " ");
}
Console.WriteLine();
return;
}
for (int idx = pos; idx < n; idx++)
{
list[now] = idx;
DoCombination(now + 1, idx + 1);
}
}
}
class Program
{
static void Main(string[] args)
{
Combination c = new Combination(7, 6);
c.DoCombination(0, 0);
}
}
정리하자면
조합은 쉽게 말하면 순서를 생각하지 않는 겁니다. 즉 (A, B)와 (B, A)를 같은 것으로 본다.
5명의 후보 중에서 2명이 후보를 뽑는 것인데 한 명은 회장, 한 명은 부회장을 뽑는 방법은 순열.
즉, 5*4 = 20가지 경우의 수
부회장 2명을 뽑는 방법은 조합
즉, (5*4) / 2 = 10가지 경우의 수
출처
[확률과 통계/순열과 조합] 순열과 조합 기본 개념 정리하기!
[확률과 통계/순열과 조합] 순열과 조합 기본 개념 정리하기! 지금 2...
blog.naver.com
(C++) 조합(Combination) 구현하기
조합이란
ansohxxn.github.io
'프로그래밍 > Algorithm' 카테고리의 다른 글
| C#으로 미로 만들기 (6) | 2023.08.24 |
|---|---|
| [프로그래머스 Programmers] 네트워크 (1) | 2023.08.24 |
| 그래프(Graph)와 트리(Tree) (2) | 2023.08.23 |
| [프로그래머스 Programmers] 소수 만들기 (5) | 2023.08.21 |
| 네이글 알고리즘(Nagle Algorithm)에 대해서 (14) | 2023.08.17 |




댓글