O(N) vs O(2N)은 동일한 시간 복잡도를 갖는다.
결론부터 이야기하자면 O(N)과 O(2N)는 동일하다.
O(N)과 O(2N)이 서로 혼동되어 다르다고 생각한다면 '입력 크기에 따라 런타임이 얼마나 빠르게 증가하는가'가 아니라 '작업 횟수'에 초점을 맞추고 있기 때문이다.
시간 복잡도는 수행시간이 아니다.
아래의 그래프를 보면서 확인해 보자
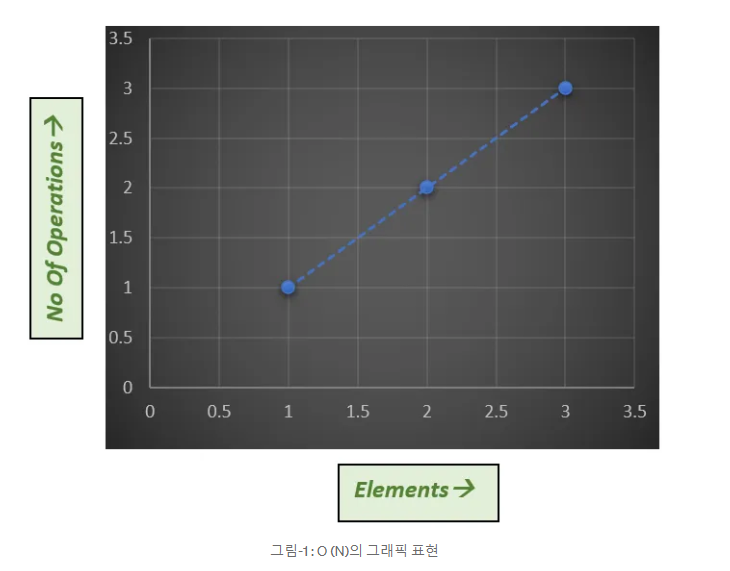

두 경우 모두 'No Of Operations'가 입력 크기에 따라 그래프가 선형적으로 증가하는 것을 볼 수 있다. 실질적으로 O(N)은 O(2N) 보다 실행 시간이 짧지만 이는 중요하지 않다. N 값이 증가하면 O(N)이 성장을 지배하게 되고 계수 2는 중요하지 않게 된다. 따라서 N의 값이 매우 커지면 둘의 실행 시간이 동일해질 것이다.
예를 들어보자
T(N) = 4N² + 3N + 9999
n = 1이나 2라면 상수 9999가 함수 성장의 상당 부분을 차지할 것이다. 하지만 N이 매우 커진다면 우리는 상수와 3N을 무시하고 4N²에만 관심을 가질 것이다. 왜냐면 대부분의 성장이 4N²에서 일어나기 때문이다. 더 나아가 N의 값이 더욱 커지면 계수 4 또한 크게 의미 없는 숫자가 되어 버린다. 그리고 우리는 O(N²)의 시간 복잡도를 가진다고 표현할 것이다.
그렇다면 왜 큰 수를 가지고 이야기를 하는 걸까?
만약 입력값이 작다면 Big-O 표기법은 별로 중요하지 않을 것이기 때문이다. 입력값이 작은데 효율성이 뭐 그렇게 중요하겠는가? 그리고 추후에 입력값이 커졌을 때 다시 수정을 하지 않기 위해서라도 큰 수를 가지고 이야기해야 한다.
정리하자면, 점근적 복잡도( asymptotic complexity)의 측면에서 O(N)과 O(2N)을 비교할 때 이 둘은 동일하다. 왜냐면 동일한 '선형적' 성장 곡선을 그리기 때문이다.
함께 읽으면 좋은 글
시간 복잡도는 수행 시간이 아닙니다.
알고리즘의 효율성을 평가하는 기본적인 척도는 시간 복잡도입니다. 문제를 풀 때에도 어떤 알고리즘이 문제의 제한을 시간 내에 통과할 수 있을지 측정하는 용도로 시간 복잡도를 제일 먼저
djm03178.tistory.com
출처
O(N) vs O(2N): Are They Same? If yes then How?
Umm… Yes! Both are same.
exploreit-askdoubt.medium.com
'프로그래밍 > Algorithm' 카테고리의 다른 글
| [프로그래머스 Programmers] 정수를 나선형으로 배치하기 (1) | 2023.12.11 |
|---|---|
| [프로그래머스 Programmers] 수 조작하기 (2) | 2023.12.05 |
| [프로그래머스 Programmers] 길이에 따른 연산 (1) | 2023.12.04 |
| O(log n) 시간 복잡도란 무엇인가? (1) | 2023.12.01 |
| [백준 BAEKJOON] 1978번 소수 찾기 (0) | 2023.11.29 |




댓글