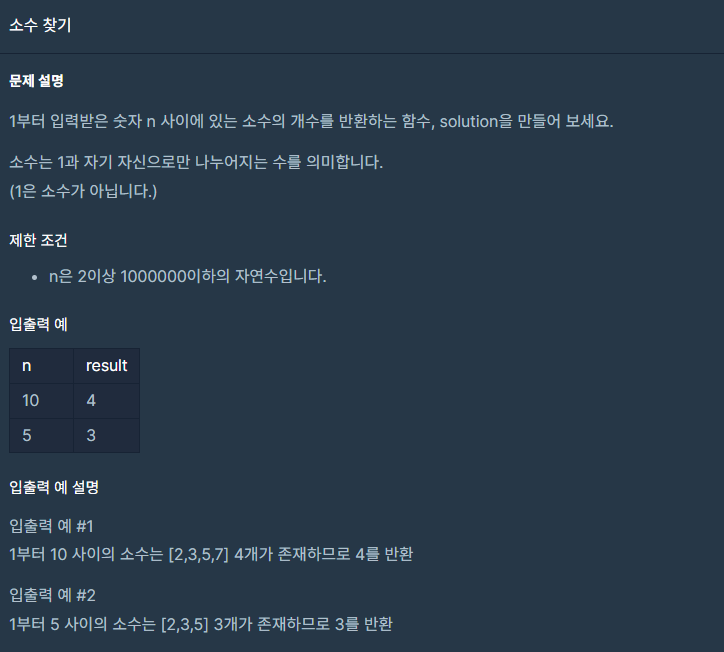
문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한 사항
n은 2이상 1000000이하의 자연수입니다.
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
1차 풀이 코드 실패 (에라토스테네스의 체로 풀어봄)
public class Program
{
static void Main(string[] args)
{
List<int> primeList = new List<int>();
List<int> list = new List<int>();
for (int i = 2; i < 1000000; i++)
{
if (GetPrime(i))
{
primeList.Add(i);
}
}
int n = 10;
for (int i = 2; i <= n; i++)
{
list.Add(i);
}
list.RemoveAll(x => IsPrime(2, x) == false);
list.RemoveAll(x => IsPrime(3, x) == false);
list.RemoveAll(x => IsPrime(5, x) == false);
list.RemoveAll(x => IsPrime(7, x) == false);
list.RemoveAll(x => IsPrime(11, x) == false);
Console.WriteLine($"list count : {list.Count}");
}
private static int gcd(int n, int m)
{
while(m > 0)
{
var r = n % m;
n = m;
m = r;
}
return n;
}
private static bool GetPrime(int num)
{
for (int i = 2; i <= 1000000; i++)
{
if (num == i) continue;
if (num < i) return true;
if (num % i == 0)
{
return false;
}
}
return true;
}
private static bool IsPrime(int m, int num)
{
if (m == num) return true;
if (num % m == 0)
{
return false;
}
return true;
}
}
2차 풀이 코드 실패 (2에서 n / 2까지 약수인지 확인)
using System.Collections.Generic;
public class Solution {
public int solution(int n) {
List<int> list = new List<int>();
for (int i = 2; i <= n; i++)
{
if (IsPrime(i))
{
list.Add(i);
}
}
return list.Count;
}
private static bool IsPrime(int n)
{
for (int i = 2; i <= n / 2; i++)
{
if (n == i) continue;
if (n % i == 0)
{
return false;
}
}
return true;
}
}
시간 복잡도가 선형 시간으로 늘어나서 효율성 테스트 실패
O(n)
단순하게 n까지 확인해서 해당 수로 나눠지는 지를 확인해본다.당연하게도 실패
O(n/2)
2차 시도는 n/2만큼까지 확인해서 해당 수로 나눠지는 지를 확인해본다. 이때 당시에는 O(n)은 O(n/2)와 시간 복잡도가 동일하다는걸 알지 못했다.
O(N) vs O(2N): Are They Same? If yes then How?
Umm… Yes! Both are same.
exploreit-askdoubt.medium.com
3차 풀이 코드 실패 (2에서 Sqrt(n)까지 약수인지 확인)
using System;
public class Solution {
public int solution(int n) {
int answer = 0;
for (int i = 2; i <= n; i++)
{
if (IsPrime(i))
{
answer++;
}
}
return answer;
}
private static bool IsPrime(int n)
{
for (int i = 2; i <= Math.Sqrt(n); i++)
{
if (n % i == 0)
{
return false;
}
}
return true;
}
}
O(√n)
n / 2로 최적화를 시도했지만 효율성에서 실패
IsPrime 함수 내에서 i의 제곱근보다 클때까지만 진행하도록 수정
풀이 코드 (2에서 제곱근까지 약수인지 확인)
using System;
public class Solution {
public int solution(int n) {
int answer = 0;
for (int i = 2; i <= n; i++)
{
if (IsPrime(i))
{
answer++;
}
}
return answer;
}
private static bool IsPrime(int n)
{
for (int i = 2; i * i <= n; i++)
{
if (n % i == 0)
{
return false;
}
}
return true;
}
}
i * i 로 비교하든 Sqrt(n)까지 비교하든 동일하거라고 생각했지만 코드 효율성 측면에서 Math.Sqrt가 더 느리다.
- i * i <= n
- i <= Math.Sqrt(n)
O(log n)
i * i <= n은 log n의 복잡도로 동작한다.
i^2 <= n이므로 log_i n = 2로 표현이 가능하다. 베이스를 생략하고 양변을 2로 나눠주면 log n/2로 작성이 가능하다. 이때 지수가 아닌 수를 생략하므로 log n으로 표현된다.

풀이 코드 (에라토스테네스의 체)
using System;
using System.Collections.Generic;
using System.Linq;
public class Solution {
public int solution(int n) {
bool[] isPrime = Enumerable.Repeat(true, n + 1).ToArray();
for (int i = 2; i * i <= n; i++)
{
if (isPrime[i])
{
for (int j = i * i; j <= n; j += i)
{
isPrime[j] = false;
}
}
}
List<int> list = new List<int>();
for (int i = 2; i <= n; i++)
{
if (isPrime[i])
{
list.Add(i);
}
}
return list.Count();
}
}
O(n log log n) 의 복잡도를 가진다.
함께 읽으면 좋은 글
O(log n) 시간 복잡도란 무엇인가?
시간 복잡도란 무엇인가? 시간 복잡도는 입력(n)을 기반으로 알고리즘이 실행(O)되는 데 걸리는 시간을 설명한다. 시간 복잡도는 꽤나 직관적이다. 예를 들어서 O(1)의 시간 복잡도를 가지는 알고
jettstream.tistory.com
두 조건에 대해서 정리한 글
Which is more efficient inside a loop condition, i<sqrtN (pre-calculated) or i*i<N, in C++?
Suppose for a given integer N, I need to run a loop square root of N times. In C++, I can do it in these two ways like- 1) long long sqrtN = std::sqrt(N); for (long long i=1; i < sqrtN; i++) { ...
stackoverflow.com
'프로그래밍 > Algorithm' 카테고리의 다른 글
| [프로그래머스 Programmers] 개인정보 수집 유효기간 (1) | 2023.10.26 |
|---|---|
| [프로그래머스 Programmers] 신규 아이디 추천 (2) | 2023.10.25 |
| [프로그래머스 Programmers] 추억 점수 (0) | 2023.10.23 |
| [프로그래머스 Programmers] 콜라 문제 (1) | 2023.10.23 |
| [프로그래머스 Programmers] 양과 늑대 (풀이 진행중) (0) | 2023.10.18 |




댓글