만약, 지구에 종말이 온다면 남은 시간 동안 무엇을 할까?
다음은 베트남의 수도 하노이의 불교 사원에서 전해 내려오는 지구 종말에 대한 '하노이 탑' 예언이다.
고대 인도 베나레스(지금의 바라나시)의 한 사원에는 작은 구멍이 뚫린 64개의 순금 원판과 3개의 다이아몬드 기둥이 보관되어 있다고 한다. 이들 원판은 어느 것도 크기가 같지 않으며, 작은 원판이 큰 원판 위에 올라오도록 차례대로 1개의 기둥에 모두 쌓여 있다. 이 사원에서 유래되는 전설에 의하면, 수도승에게 64개의 원판을 하나씩 옮겨서 다른 기둥에 원해 상태로 부지런히 옮겨 놓으라고 명한다. (단, 원판의 이동시 작은 원판 위에 큰 원판은 올려놓을 수 없다.) 그리고 모든 원판이 다른 기둥으로 모두 옮겨질 때, 사원과 승려 그리고 지구상의 모든 것들은 먼지가 되어 사라질 것이다.

위의 예언대로라면, 지구의 종말은 얼마나 남은 것일까?
먼저 하노이의 탑을 규칙에 맞게 이동시켜 보자.
n개의 원판의 최소이동 횟수를 a(n)이라고 하면, 원판 1개에서 6개까지 최소 이동의 방법과 횟수는 아래와 같다.


이때, 최소이동 횟수에 대한 계산 규칙은 다음과 같음을 예상할 수 있다.

따라서 64개의 원판에 대한 최소이동 횟수는 a(64) = 2^64 - 1이다.
1개의 원판을 이동하는데 1초가 걸린다고 가정하면, 64개의 원판에 대한 최소이동 횟수에 대한 소요되는 시간은 a(64) = 2^64 - 1 (초)이다.
이 값은 얼마나 큰 수일까?

5,849억 년!!
하노이의 탑의 지구 종말에 대한 예언은 5,849억 년 후에 나 일어날 이야기인 것이다.
참고로 지구의 나이는 약 46억 년, 우주의 나이는 137억 년 임을 감안하면 5,849억 년이라는 시간의 느낌이 조금 더 실남이 날 수 있을까 싶다.
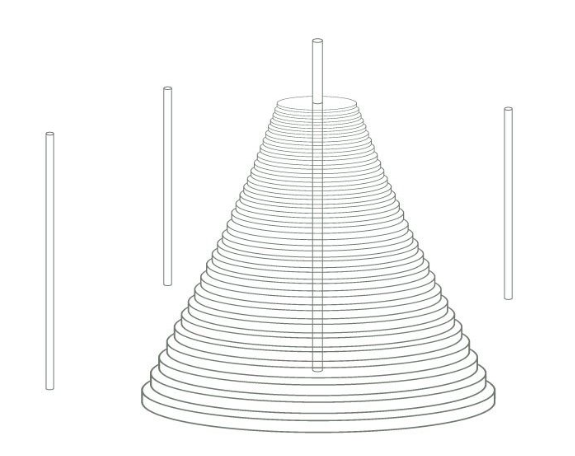
기둥이 4개인 하노이의 탑에서 n개의 원판의 최소이동 횟수를 b(n)이라고 하면, 원판 10개에 대한 최소 이동의 방법과 횟수는 아래와 같다.


기둥이 3개인 하노이의 탑 vs 기둥이 4개인 하노이의 탑

기둥이 4개인 하노이의 탑에서 64개의 원판에 대한 최소이동 횟수를 계산해 보면 b(64) = 18,433이며,
1개의 원판을 이동하는데 1초가 걸린다고 가정하면,
64개의 원판에 대한 최소 이동 횟수에 소요되는 시간은...
b(64) = 18,433(초) 약 5.12(시간)
만약 지구 종말에 대한 '하노이 탑' 예언에서 기둥이 4개였다면, 우리는 불과 5시간 만에 종말을 맞게 되는 것이다.
함께 읽으면 좋은 글
[프로그래머스 Programmers] 하노이의 탑
문제 설명 하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도
jettstream.tistory.com
출처
지구 종말에 대한 하노이 예언, 남은 시간은?
[BY LG상남도서관] 만약, 지구에 종말이 온다면 남은 시간 동안 무엇을 할까?다음은 베트남의 수도 하노...
m.post.naver.com
'프로그래밍 > Algorithm' 카테고리의 다른 글
| [프로그래머스 Programmers] 콜라츠 수열 만들기 (0) | 2024.01.03 |
|---|---|
| [프로그래머스 Programmers] 모의고사 (1) | 2023.12.13 |
| [프로그래머스 Programmers] 정수를 나선형으로 배치하기 (1) | 2023.12.11 |
| [프로그래머스 Programmers] 수 조작하기 (2) | 2023.12.05 |
| O(N) vs O(2N)은 동일한 시간 복잡도를 갖는다. (1) | 2023.12.05 |




댓글