그래프(Graph)란 무엇인가?
- 정점(Vertex)과 그 정점을 연결하는 간선(Edge)을 하나로 모아 놓은 자료구조.
- 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조
- G = (V, E)
ex. 지도, 지하철 노선도, 전기 회로의 소자들, 도로 등
그래프의 종류
무방향 그래프(Undirected graph)
두 정점을 연결하는 간선에 방향이 없는 그래프, 두 정점의 양 방향으로 이동 가능

방향 그래프(Directed graph)
두 정점을 연결하는 간선에 방향이 있는 그래프. 특정 방향으로만 이동 가능
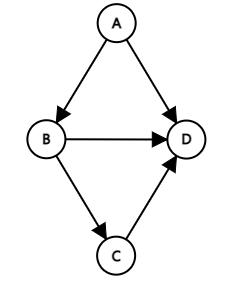
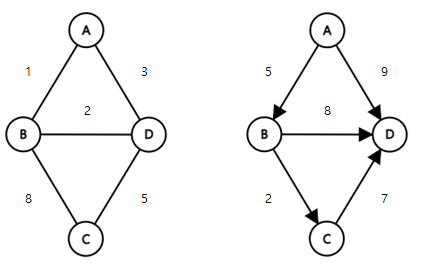
가중 그래프(Weighted graph)
정점을 연결하는 간선에 가중치(Weight)가 있는 그래프. 네트워크(Network) 라고도 함
완전 그래프(Complete graph)
그래프의 모든 정점이 1:1 간선으로 연결된 그래프

연결 그래프(Connected graph) vs 비연결 그래프(Unconnected graph)
모든 정점 사이에 간선이 존재하는 그래프를 연결 그래프, 간선이 하나라도 존재하지 않는 그래프를 비연결 그래프라 함.

그래프 구현 방법
인접행렬(Adjacency matrix)
2차원 배열을 이용하여 인접 행렬은 상대적으로 정점의 개수가 적고, 간선의 수가 많을 때 사용하는 것이 좋다.
정점 i와 j를 잇는 간선이 존재한다면 [i][j] = 1, 간선이 존재하지 않는다면 [i][j] = 0
장점
- 두 정점 사이의 간선 정보를 확인하는 것이 빠르고, 새로운 간선을 추가하고 제거하는 것이 빠르다.
단점
- 간선의 개수와 관계없이 배열의 크기가 항상 n*n(n은 정점의 개수)이므로 메모리를 많이 사용한다.
- 노드를 추가, 제거하는데 오래 걸림
- 특정한 노드에 인접한 노드를 찾기 위해 모든 노드를 순회
- 그래프의 모든 간선의 수를 찾기 위해 모든 노드를 순회
인접 리스트(Adjacency List)
1차원 배열(시작 정점을 기준으로 정점의 개수만큼 연결 리스트가 1차원 배열에 저장)
배열의 크기는 정점의 개수와 같음
인접 리스트는 정점의 개수가 많고 간선의 개수가 상대적으로 적을때 사용하는 것이 좋다.
장점
- 노드의 수가 아닌 간선의 수에 따라 메모리 사용량이 달라지기 때문에 메모리 효율이 좋음
- 특정 노드에 직접 겁근할 수 있어 인정한 노드를 찾기가 쉬움
- 노드의 추가, 삭제가 빠름
- 새로운 간선 추가에 빠름
- 그래프의 모든 간선의 수를 찾는 것이 빠름
단점
- 두 노드의 간선 정보를 확인하는데 오래 걸림
참고 사이트
[C# 기초] #19.Graph - Graph의 정의, 종류, 구현 방법
1. Graph란? 정점(vertex(V))과 그 정점을 연결하는 간선(edge(E)을 하나로 모아 놓은 자료구조. 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조입니다. G = (V, E) (ex) 지도, 지하철 노선도, 전기
geukggom.tistory.com
'프로그래밍 > Algorithm' 카테고리의 다른 글
| 스택(Stack) 자료구조 (1) | 2023.08.30 |
|---|---|
| 너비 우선 탐색(Breadth-first search, BFS) (2) | 2023.08.30 |
| [프로그래머스 Programmers] 배달 (2) | 2023.08.29 |
| 방향 배열(Direction Array)로 간편하게 상하좌우 배열 이동하기 (1) | 2023.08.25 |
| C#으로 미로 만들기 (6) | 2023.08.24 |




댓글