지수(exponent)란 무엇인가?

위에 표시된 숫자들을 우리는 2의 3승, 혹은 5의 세제곱 등과 같이 읽는다. 요새는 몇 제곱과 같이 표현을 하겠지만, 예전에는 몇 승(升)이라고 표현했다. 몇 승이라는 표현도, 위에 숫자가 알라탄 것과 같은 모습이기에 나름 비슷한 이미지를 주는 것 같긴 하다. 이와 같은 승수, 제곱으로 표현되는 수를 지수(exponent)라고 한다.
지수와 지수의 밑은 아래와 같다.

오른쪽 위의 작은 숫자를 지수(exponent)라고 부르고 지수 밑에 있는 큰 숫자를 밑이라고 부른다.
이 예제에서는 4가 밑(base)이고 3이 지수(exponent)이다.
아래의 수는 밑이 7이고 지수가 5인 수이다.

지수는 밑수를 몇 번 곱해야 하는지 나타내는 수이다. 이 예제에서 4^3은 밑인 4를 3번 곱해야 한다는 것을 의미한다.

곱셈식으로 표현하면 이것을 쉽게 계산할 수 있다. 위 예제를 이렇게 계산해 보자:
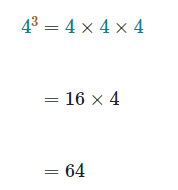
지수를 사용하는 이유는 큰 수를 좀 더 간단하게 나타낼 수 있기 때문이다. 아래의 예를 살펴보자.

쓰려면 손이 아플 정도로 정말 길다. 2를 6번 곱한 식으로 나타내기보다 2를 밑으로 쓰고 6을 지수로 쓰면 더 간단하게 나타낼 수 있다.
로그(log)란 무엇인가?
로그는 지수를 다른 방법으로 표현한 것이다.
예를 들어, 2의 4 제곱은 16이라는 것을 알고 있다. 이것은 지수방정식 2^4 = 16으로 나타낼 수 있다.
이제, 누군가가 이렇게 물어볼 것이다. "2를 몇 제곱해야 16이 되나요?" 정답은 4일 것이다. 이것은 로그방정식 log_2(16) = 4로 나타낼 수 있으며, "2를 밑으로 하는 16의 로그방정식은 4"라고 읽는다.

두 방정식 모두에서 2,4,16의 관계가 동일하게 표현된 것을 알 수 있다. 2는 밑이고 4는 지수이다.
지수방정식은 진수 16과 분리된 형태이지만, 로그 방정식은 지수 4와 분리된 형태이다.
다음은 서로 같은 의미를 같은 로그방정식과 지수방벙식의 예이다.
로그의 정의
위의 일반화된 예시를 통해 로그의 정의를 알 수 있었다.

두 방정식 모두에게 a, b, c의 관계를 동일하게 나타내고 있다.
- b는 밑
- c 는 지수
- a는 진수입니다.

문제 풀이

정답 : A

정답 : B

정답 : 4^2=16

정답 : 2^6=64
출처
지수란? (개념 이해하기) | 지수 (중등1학년) | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org
로그란? (개념 이해하기) | 로그 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org
'프로그래밍 > 수학' 카테고리의 다른 글
| 숫자 10은 허상이다 (0) | 2024.01.22 |
|---|---|
| 1e+6 이게 뭔데? 과학적 표기법이란 무엇인가? (1) | 2023.12.29 |
| 각의 종류 (0) | 2023.09.27 |
| 약수와 배수 (0) | 2023.09.12 |
| 집합 기호와 명제 기호 간의 상호번역 (0) | 2023.09.08 |




댓글