다항식 곱하기

다항식 곱하기

두 개의 다항식의 곱 (a + b)(c + d)를 곱한다고 한다면

 

(a + b)를 m으로 치환하고 나서 분배 법칙을 적용해 보자.

 

(a + b)(c + d)

= m(c + d)

= (m x c) + (m x d)

= ((a + b) x c) + ((a + b) x d)

= ac + bc + ad + bd 

 

ac + ad + bc + bd

 

이런 방식으로 만약 (a + b)²를 계산한다면 어떻게 될까요?

 

(a + b)(a + b)

= m(a + b)

= (m x a) + (m x b)

= ((a + b) x a) + ((a + b) x b)

= a² + ab + ab + b²

= a² + 2ab + b²

 

$$ (a + b)^2 = a^2 + 2ab + b^2 $$

$$ (a - b)^2 = a^2 - 2ab + b^2 $$

 

도형이 커진 부분에 대해서 더해주면 이해하기 쉽다.

 

이런 방식으로 만약 (a - b)²를 계산한다면 어떻게 될까요?

 

(a - b)(a - b)

= m(a - b)

= (m x a) - (m x b)

= ((a - b) x a) - ((a - b) x b)

= a² - ab - ab + b²

= a² - 2ab + b²

 

도형이 줄어든 부분을 빼주면 이해하기 쉽다.

(a - b)2의 경우 도형이 줄어든다.

큰 파랑 사각형 a²에서 노란 영역을 빼준다고 가정한다면 아래와 같이 쓸 수 있다.

 

= a² - (b(a - b) + b(a - b) + b²)

= a² - ((ab - b² + ab - b²) + b²)

= a² - (2ab - 2b² + b²)

= a² - (2ab - b²)

= a² - 2ab + b²

다항식 세제곱하기

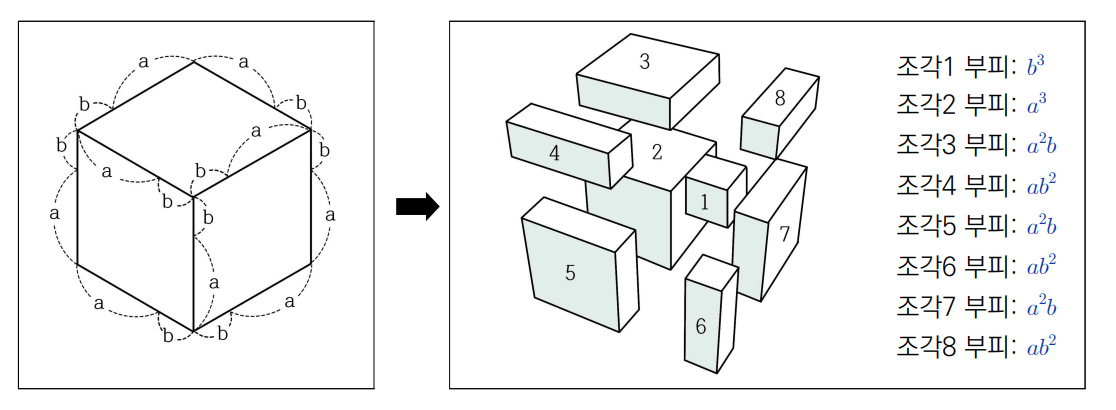
다항식의 곱 (a + b)(a + b)(a + b)를 곱한다고 한다면 2차원이었던 도형이 이제 3차원으로 확장된다.