조합(Combination)의 성질
예를 들어, 10개의 서로 다른 사탕 중 3개를 뽑아서 먹어버리면 7개가 남게 된다.
즉, 10개 중에 3개를 뽑는 방법의 수와 10개 중 7개를 남기는 방법의 수는 같다.
- 첫 번째 성질
$$ _{n}\mathrm{C}_{r} = _{n}\mathrm{C}_{n-r} $$
일반화하면 전체 n 개 중에서 r개를 뽑으나 n-r개를 남기나 경우의 수는 같게 된다는 것이다. 계산으로도 간단히 확인할 수 있으니 증명은 쿨하게 생략하도록 하겠다.
이 성질은 조합의 계산을 간단하게 만들어준다. 10C7 보다 10C3이 훨씬 계산하기 쉽기 때문이다.
9C1 = 9C8
2C1 = 2C1
- 두번째 성질
$$ _{n}\mathrm{C}_{n} = 1,_{n}\mathrm{C}_{0} = 1 $$
nCn은 n개 중에서 n개를 다 뽑는 방법의 수이기 때문에 경우의 수는 당연하게도 1이 된다.
nC0은 n개 중에서 0개를 뽑는 방법의 수이기 때문에 이 또한 1이 된다.
- 세번째 성질
$$ _{n}\mathrm{C}_{r} = _{n-1}\mathrm{C}_{r-1} + _{n-1}\mathrm{C}_{r} $$
10명의 부원으로 이루어진 농구부가 있다고 가정해 보자. 그중 한 명은 에이스이다.
슛을 던졌다 하면 골인에, 리바운드와 수비까지 최정상급인 선수이다. 단, 체력이 약하다는 단점이 있다.
이제, 경기에 출전할 5명의 선수를 선발해야 하는데, 감독의 생각은 이렇다.
- 처음부터 에이스를 투입해서 점수를 따고, 후반에 수비 잘하는 선수와 교체해야 할까?
- 처음엔 에이스 빼고 가고 후반에 상대가 지쳤을 때 에이스를 투입해서 역전을 노릴까?
첫 번째 경우라면 에이스는 이미 뽑혔으므로(n-1) 나머지 9명 중 4명을 뽑으면 된다. (n-1Cr-1)
두 번째 경우라면 에이스를 제외한 나머지 9명에서 선발 출장할 5명을 뽑으면 된다. (n-1Cr)
첫 번째와 두 번째 경우의 수를 합치면 전체 10명 중 5명을 뽑는 경우의 수가 된다.
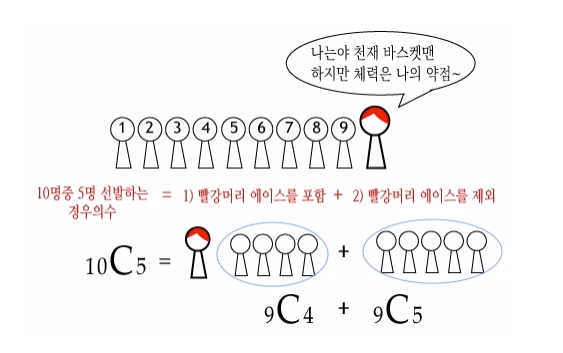
다시말해, 전체 n명중 r명을 선택하는 방법을 특정한 사람을 포함한 경우와 포함하지 않는 경우로 나눈다.
특정한 사람을 포함한 경우라면 나머지 n-1 명 중 추가로 r-1명을 선택하면 된다. >> n-1Cr-1
특정한 사람이 포함되지 않는 경우는 나머지 n-1명 중 r명을 선택하면 된다. >> n-1Cr
이 두 가지를 합하면 결국 n 명중 r명을 선택하는 경우의 수가 된다.
이 세 번째 성질은 조합을 재귀로 구현할 때 바로 사용이 가능하다.
함께 읽으면 좋은 글
C# [백준 BAEKJOON] 2407번 조합
문제 nCm을 출력한다. 입력 n과 m이 주어진다. (5 ≤ n ≤ 100, 5 ≤ m ≤ 100, m ≤ n) 출력 nCm을 출력한다. 2407번: 조합 n과 m이 주어진다. (5 ≤ n ≤ 100, 5 ≤ m ≤ 100, m ≤ n) www.acmicpc.net 풀이 코드 해당 문
jettstream.tistory.com
출처
조합의 성질 다시 보기
이번 포스트에서는 조합이 가지고 있는 몇 가지 성질들을 살펴보려고 합니다. 몇몇 참고서에서는 "조합의 ...
blog.naver.com
'프로그래밍 > 수학' 카테고리의 다른 글
| 지수(Exponent)와 차수(Degree) (0) | 2024.05.03 |
|---|---|
| 소인수 분해 용어 정리 (2) | 2024.05.02 |
| 다항식 곱하기 (1) | 2024.04.03 |
| 항, 상수항, 계수란 무엇인가? (1) | 2024.04.03 |
| 2는 유일한 짝수 소수(even prime number)이다. (1) | 2024.04.02 |




댓글