집합론(集合論, set theory)에 대해서
함수형 관련 프로그래밍을 공부하다 보니 수학에 대해서 조금씩 공부하고 있다. 오늘은 집합론에서 다루는 정의역, 공역, 치역에 대해서 알아보려고 한다.
정의역(定義域, domain)
역은 '영역, 구역'을 뜻한다. 정의역은 '함수가 정의된 영역'을 말한다. 즉 함수에 입력되는 인자를 뜻한다.
공역(共域, codomain)
공은 공동, 공통, 공존 등에 쓰이는 한자로 함께라는 뜻이다. 공역은 '정의역'에 대응하는 영역'이라는 의미로, 함숫값이 존재하는 영역이다.
치역(値域, range)
치는 가치, 수치 등에 쓰이는 한자로, '값'이란 뜻이다. 여기서 값이란 함수의 값을 말하며, 치역은 함숫값의 범위를 뜻한다.
실제로 함수에 정의역을 입력해서 나온 값의 범위를 의미한다.
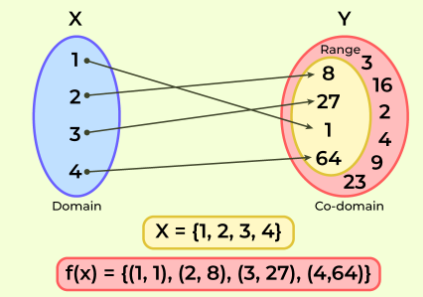
치역은 공역의 부분 집합이다
함숫값은 공역 위에 존재하므로, 함숫값의 집합인 치역은 공역에 포함되는 부분집합이다. 치역과 공역이 같다면, 그 함수를 전사 함수(surjective function)라고 부른다.
참조 사이트
024. 정의역 vs 공역 vs 치역
# 정의역 | 定義域 | domain **역**은 '영역, 구역'을 뜻한다. 정의역은 '함수가 정의된 영역'이다. # 공역 | 共域 | codomain **공**은 공동, 공통,…
wikidocs.net
Domain and Range| How to Find Domain and Range of a Function? - GeeksforGeeks
Domain and Range are the input and output values of a Function. Learn how to find Domain and Range of a Function in this article. Unlock the world of mathematical functions with our Domain and range calculator. From understanding Domain and range of a gra
www.geeksforgeeks.org
'프로그래밍 > 수학' 카테고리의 다른 글
| 2는 유일한 짝수 소수(even prime number)이다. (1) | 2024.04.02 |
|---|---|
| 정수의 기하학적인 성질 (0) | 2024.03.19 |
| 통분에 대해서 알아보자 (0) | 2024.03.12 |
| 합의 법칙과 곱의 법칙 (1) | 2024.03.06 |
| 팩토리얼(Factorial, 계승)과 순열의 관계 (2) | 2024.03.06 |




댓글